On the 3rd of August, 2004 a Delta II rocket launched the MESSENGER spacecraft on its voyage of exploration toward the planet Mercury [Fig. 2]. More than 6 1/2 years later on the 17th of March, 2011 MESSENGER inserted itself into orbit around the planet. The journey was a long one… nearly 8 billion kilometers. It included one Earth flyby, two Venus flybys and three Mercury flybys before parking itself into an elliptical orbit around Mercury. [Johns Hopkins 2008]
Why did it take so long? Mercury's orbit takes it to roughly the same distance from the Earth as Mars but a coasting trip to Mars takes only between 6 and 11 months. There were two reasons… physics and cost.
The planet Mercury orbits the sun in an elliptical orbit with a semimajor axis of ≈ 0.39 AU, an orbital period of 88 days, and importantly, an orbital velocity of 47.9 km/s. By comparison, the Earth has an orbital velocity of just 29.8 km/s.

Figure 1 MESSENGER orbital trajectory [NASA]
So one of the biggest challenges that the designers of the MESSENGER spacecraft mission had to solve was getting the spacecraft to catch up to Mercury but not blow past it. The difference in velocities is 18.1 km/s. For the probe to accelerate to Mercury’s orbital velocity is not the issue since it will “fall” into the sun’s gravitational well. The issue is managing the velocity so that it slows down enough to do a tangential orbital insertion and that requires either a lot of propellant or the very clever use of physics. Given MESSENGER’s tight energy budget meeting the target required careful maneuvering and mission planning. [McAdams 1998]
Building and launching a spacecraft that can accelerate rapidly is not an insurmountable problem however doing so within anemic fiscal budget constraints can make the challenge formidable. Clearly the mission planners for MESSENGER had to accomplish lofty mission objectives at a minimum cost or risk facing program cancellation. So they had to be ingenious and take advantage of what nature has provided in the form of gravity assists. The trade-off is mission time. These kinds of trade-offs exist as considerations for virtually all missions of space exploration.

Figure 2 MESSENGER launch aboard a Delta II [Boeing]
In this paper I will examine the challenges of interplanetary spacecraft propulsion systems and mission designs of today’s, as well as future vehicles.
Navigating in Space
Interplanetary travel requires careful energy management. Let's say that we’re planning for a mission to Mars. The first thing the mission planner needs to understand is that the launch platform, namely the Earth, is moving with respect to the faraway destination, and that too is moving. Secondly, he needs to understand that massive objects like the Sun or the planets create their own "gravity wells" that the probe will need to either “fall into” or “climb out” of. These maneuvers require energy and that is usually in limited supply.So, let's get back to our mission to Mars. If we were to take our rocket and simply point it at the planet then push the throttles to the firewall our mission would likely be lost into deep space. Like a competitive trap shooter the trajectory designer has to consider that Mars is moving and he will need to “lead” the planet so that Mars’ orbit intersects the probe's trajectory. He also will need to factor in enough thrust to climb out of the Earth's gravity well as well as providing for enough thrust to decelerate when falling into Mars’ gravitational well to enter orbit.
The mission planner must consider that fuel carried is also additional mass that needs to be accelerated. In other words, the shorter the mission time for a given distance, the more fuel needs to be carried, and the more fuel that needs to be carried means incremental thrust requirements, and additional thrust means requiring more fuel. This is an exercise in economics.
So our Mars mission planner looks for the most fuel-efficient way to get to the Red Planet and decides to use a technique known as the Hohmann transfer orbit, named after Walter Hohmann. [Wiki 2011]
Hohmann Transfer Orbit
The low energy Hohmann transfer orbit is the most fuel-efficient.
Figure 3 Hohmann transfer orbit diagram [Wikipedia Commons]
Here's how it works. Look at the coplanar diagram above. The green circle is the orbit of the earth. The red circle is Mars’ orbit. The probe initiates a trans-planetary burn that is roughly tangential to the orbit of the Earth. Keep in mind that at this point the Earth and the spacecraft have an orbital velocity that is essentially “free” angular momentum. The probe's burn puts the spacecraft in a highly elliptical orbit with the Sun at one focal point (the yellow elliptical orbit). Mission planners will time the burn so that the probe arrives at Mars coincident with the probe’s aphelion and with an orbital velocity which is roughly equal to that of Mars. The difference between the initial orbital velocity at the probe's departure and the arrival orbital velocity is known as delta-v. After the initial burn the probe will coast to Mars in the no friction environment of space. [JPL 2011]
On June 2nd of 2003 the European Space Agency launched the Mars Express it attained Mars orbit on Christmas Day of the same year. That was a relatively fast 6 1/2 month trip that covered 400 million km (even though the mission was plagued with navigation problems and was hit by massive solar flares). One of the factors determining the speed of the mission’s coast phase was the alignments of Mars and Earth in 2003 that were the closest that they had been in over 60 millennia.
In order to complete the transfer the spacecraft must initiate a second corrective burn in order to place it into a roughly circular orbit otherwise it will simply continue on its initial orbit and head back to the Sun.
The last step is known as orbital insertion and the spacecraft will make final adjustments to place it in an orbit around Mars.
This is a fuel-efficient trajectory; however it does place limitations on mission planners. The biggest limitation is the launch window. Essentially these are “windows of opportunity” where the Earth and the destination planet are in the correct alignment for the Hohmann transfer to result in a rendezvous. Unless the orbital alignments match, the probe arrives at its aphelion and Mars isn't there. The planet will be either too far ahead or too far behind the spacecraft.
Going to Mars using the Hohmann transfer orbit requires capitalizing on planetary alignment opportunities that are periodic. Mars and the Earth arrive at the same position in their orbits relative to each other once every 2.135 years this is known as the synodic period. That means the launch window recurs only every 780 days and remains open for only a couple of weeks. This is a critical consideration especially when it comes to manned spaceflight. If we travel to Mars we can't just turn around and come home if something goes wrong.
Mission planners use what are known as porkchop plots [Fig. 4] to assist in planning optimal launch windows. These charts show contours of equal characteristic energy, or C3, against specific combinations of launch and insertion dates for any given interplanetary flight. C3 is a measure of the energy required for a mission that requires attaining an excess of orbital velocity over and escape velocity required for additional maneuvers. [Sellers 2005]
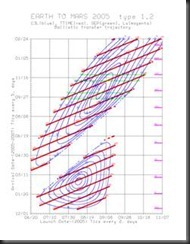
Figure 4 Porkchop plot for a Mars 2005 mission [NASA]
Delta V
Knowing when to launch is only part of the problem, the other part is knowing how to manage your velocities and T2/a3 = k (Kepler's 3rd Law).When you light up your initial burn you need to be sure to add enough delta-v to carry the spacecraft to Mars in time to intercept and match orbital velocities.
Calculating the departure and arrival delta-v ‘s as well as the transfer time are pretty straightforward. [
Delta-v departure (instantaneous burns)

The delta-v for the Mars transfer orbit works out to approximately 0.6 km/s.
Delta-v arrival (instantaneous burns)

The delta-v for Mars capture where the highly elliptical Hohmann orbit is circularized 0.9 km/s.
Total delta-v
Combine the two for a total delta-v of 1.5 km/s.
Time of transfer (Hohmann)

The time of transfer works out to .708 years or just under 8 months 3 weeks.
Again, the biggest disadvantage of low-cost, high fuel efficiency is that these missions can be ponderously slow, with missions taking years instead of months and launch windows can be few and far between.
Type I and Type II Trajectories
More direct trajectories that carry the spacecraft less than 180° around the Sun are called Type I trajectories if it's more than 180° they are Type II trajectories.A couple of notes are in order about shaping a spacecraft’s orbit… If there is a burn somewhere in the vehicle's trajectory the shape of the orbit will change however the spacecraft will return to that same point on every subsequent go around. So if a mission planner wanted to increase the altitude of a circular orbit above the planet and not just change the periapse or apoapse of an orbit than two short burns will be required to shape the orbit.
If a vehicle is in a circular orbit and the rocket is fired in the direction of travel, effectively slowing the vehicle down as if it was retro rocket, the new orbit will be elliptical with a lower periapse, 180° opposite the firing point. When that new periapse dips into the planet’s atmosphere then that becomes a reentry maneuver. [Fig. 5]
Lastly it's important to discuss when to burn. You want to use your probe's rocket engine to burn when the craft is traveling at higher speed because it generates much more useful energy than at low speed. This is known as the Oberth Effect. This effect occurs because the propellant has more usable energy when kinetic energy is added to chemical potential energy to produce more useful mechanical energy. So in an elliptical orbit you would want to plan a burn for periapsis when the craft's KE is higher in MGH is lower. Understanding how to utilize the Oberth Effect was considered revolutionary in understanding that enormous tank mass of fuel was not required for effective interplanetary travel.

Figure 5 Apollo capsule reentry [NASA]
Newton’s 3rd Law
So now we know how much delta-v is required to initiate the transfer and how much is required to put the probe into a circular orbit (around the sun prior to any Mars orbital insertion maneuver). How do we determine what type, and how long, of burn will produce the required delta-v.Newton's third law states that for every action there is an equal and opposite reaction. With few exceptions most every space propulsion system in the worldwide inventory are reaction based chemical rockets. That means that mass is accelerated to high velocities and expelled out one end of the spacecraft and inducing a reaction force vectored in the opposite direction producing thrust and acceleration.
The formula that relates delta-v to the rocket’s exhaust velocity and the difference in its mass at the beginning of his burn and end of its burn is known as the ideal rocket equation, also called the Tsiolkovsky rocket equation. The equation is…
where
So to produce the required delta-v we need to accelerate enough mass out the nozzle of our engine with sufficient velocity to give our spacecraft the thrust necessary to make the transfer.
The thrust of a bipropellant pumped liquid rocket is expressed as…
where
ve is exit velocity
pe is the exit pressure
po is the outside pressure
Ae is the area of the exit
In the case of liquid oxygen and liquid hydrogen (LO2 + LH2) the exhaust velocities can get to as high as 4,500 m/s.
How much thrust a rocket produces in one second is known as its specific impulse. That is a measure of the efficiency of your rocket propellant.
What it really comes down to is how quickly can you get a lot of mass out the rear of the spacecraft and at what velocity? That will determine the thrust and that in turn determines your delta-v . And that… determines whether or not you get to Mars.
Our little Mars bound spacecraft uses a chemical rocket for its primary propulsion. Simple in principle, it reacts one or more propellants together to produce a high velocity directed exhaust that exits the spacecraft through a specially shaped nozzle which enhances thrust through thermodynamic expansion. Some rockets, such as the Space Shuttle's main engines react oxygen and hydrogen together to produce massive volumes of high velocity steam. Others use a mixture of kerosene and liquid oxygen. Smaller attitude control thrusters may use hypergolic fuels such as hydrazine or compressed gasses.
Typically, solid fuel rockets are not used in spacecraft propulsion except in launch boosters. Solid fuel rockets are stable and exceptionally reliable however they cannot be throttled in-flight and once lit they burn to completion.

Figure 6 Shuttle launch [NASA]
(Note the photograph of a shuttle launch in figure 6. The exhaust coming from the three main engines is invisible since it is high temperature steam. Now compare that to the fiery plume of the twin solid rocket booster’s exhaust.)

Figure 7 A liquid fueled rocket engine [NASA]
All reaction propulsion systems need to carry their fuel with them. It's that mass that is expelled from the rear to produce an opposite forward thrust. [Fig. 7] Unfortunately, that exacts a penalty on mission planners since the fuel that makes the rocket go, first needs to be carried up to the spacecraft and it’s heavy. It's called the tank mass and that has to be added to the structural mass of the vehicle plus the payload. For a given amount of thrust if you have too much tank mass your thrust to weight ratios will be way off and you're acceleration will be poor. That may cause you to supply insufficient delta-v to complete your mission. So keeping weight down and keeping fuel requirements to an absolute minimum are essential design considerations. So how do you carry enough fuel to get to Mercury? Answer, you get nature to help out.
Gravity Assists
If one were to look at space away Einstein did he would see that the fabric of space-time has a topology.
Figure 8 Interplanetary superhighway [NASA]
Borrowing the famous rubber sheet analogy just imagine the Sun and the orbiting planets being heavy masses resting on a rubber sheet stretched tight. The more mass there is the more space-time around it is deformed. So the Sun would be like a bowling ball and the inner planets like golf balls bending and stretching the space around them. Objects traversing this interplanetary space need to be "cognizant" of the topology. Moons, comets, space probes and even light follows the same geometry. The “rubber sheet” that is the fabric of space-time has planes and valleys, dimples and wells.
Since keeping fuel consumption to a minimum is a primary objective, mission designers have found a way to use a planet’s gravitational tug to transfer angular momentum from the planet to a spacecraft in a maneuver called a gravity assist flyby.

Figure 9 Mariner 10 flybys 1973-1974
This very cool maneuver was developed in 1961 by a UCLA grad student named Michael Minovitch while he was working a summer job at the Jet Propulsion Laboratory.
While working on another problem, Minovitch realized that you could travel almost anywhere in the solar system by using the gravitational fields of other bodies to catapult your vehicle to distant targets without using any additional propulsion. The energy requirements were even lower than those of the Hohmann "minimum-energy" co-tangential trajectories discussed earlier.
It works something like this. If you directed your probe to just to skirt by the planet Venus the spacecraft would begin to accelerate as it enters Venus’ gravity well. It would continue to pick up speed until it passes the planet and decelerates as it climbs out of the same gravitational well. Taken in isolation, the velocity at the beginning of the encounter would be exactly the same as the velocity at the end. There's no gain.
However, the planet Venus is not static. It too is orbiting the sun with a mean orbital velocity of 35 km/s. As your spacecraft approaches the planet some of Venus’ angular momentum is lost to the probe. In physics this is called an elastic collision in that the momentum is fully transferred from one body to the other even though there is no direct contact between the probe and the planet. The angular momentum that the probe gains (due to the conservation of angular momentum) results in an increased delta-v. This relationship is best visualized by using the vector addition model shown in figure 9. Note the resultant vectors.

Figure 8
MESSENGER’s mission planners had to find a way to reduce the probe’s delta-v while conserving its scarce supply of onboard propellant. Also, since the spacecraft is navigating through three-dimensional space the astrogators could use the six gravity assists not only to change the probe’s velocity but also to reshape the orbit… either to more circular or more elliptical and even adjust the orbit’s tilt and rotation.
At one point MESSENGER’s velocity increased to 62.6 km/s while sliding down the Sun’s deep gravitational well!
Using Minovitch’s gravity assist maneuver and theory of space travel we have been able to send missions to all the planets. [Minovitch 1997] The missions have included the Mariner series, Pioneer, the Voyager’s, Galileo, Cassini, MESSENGER and recently the New Horizons mission to Pluto.
Changing the magnitude of the spacecraft’s velocity through gravity assist is called "orbit pumping." Using gravity to change the spacecraft's trajectory relative to the planet’s orbital plane is called “orbit cranking.” Most interplanetary missions use both techniques.
Before the gravity assist technique was developed the only way that mission planners foresaw the ability to travel to deep space destinations was through the development of exceedingly large and expensive nuclear rockets.
Mission Planning
So what are some of the principal considerations when designing a mission? It all starts with the payload. What type of payload? How big is the payload? Where is it going? How fast does it need to get there? What are the range of operating temperatures? Is it an instrumental mission or a manned mission? What are the power requirements? Is it a flyby, an orbital insertion mission, or a landing? Does the mission plan to return to the Earth or is it a one-way trip? Is it returning with samples or people? Is there a tight launch window? Most important, what's the budget?Once these objectives have been identified the designers can get to work in engineering the attitude and orbit control subsystems, the communications and data handling subsystems, environmental control and life support subsystems (for manned missions), structure and mechanisms, propulsion subsystems, and electrical power subsystems. Adjustment to these systems can take multiple iterations. [Sellers 2005]
New Propulsion Systems for Interplanetary Missions
So far the only propulsion system that we have discussed has been chemical reaction rockets. Chemical propellants pack a lot of energy for a given mass but they are massive and given the limitations of fuel supply that can only be fired in short bursts. So alternative electrodynamic propulsion systems are being developed and they include ion electric, Hall effect and pulsed- plasma thrusters.An ion drive uses electrical energy from solar panel or on-board nuclear sources to accelerate charged particles out the nozzle of a spacecraft at high velocities rather than the heat supplied from an exothermic chemical reaction. By comparison to chemical propulsion ion drives produce very low thrust but that thrust can be sustained for very long periods of time. In the low friction environment of space the acceleration is cumulative.
The way an ion engine works is to take a gas and strip it of its electrons, ionizing it. Ions are charged particles that can be accelerated by electrical and magnetic fields to extremely high velocities. Then in response to Newton's 3rd law the spacecraft accelerates in the opposite direction. The energy required to ionize the gas and accelerate it can be supplied by solar panel arrays or from nuclear sources.

Figure 9 Deep Space One [NASA]
The Deep Space One [Fig. 10] mission was a demonstrator of ion electric propulsion systems. It used the inert gas xenon as its ion source. A pair of grids in the engine charged to almost 1300 V of potential accelerated the ions to very high velocities. Those velocities approached 40 km/s. That's almost 9 times higher velocities than the H2 + O2 reaction of a bipropellant chemical rocket.
So although the thrust is low it can be sustained not for minutes but for months or even years. The Deep Space One test vehicle used 74 kg of propellant and sustained its thrust for 678 days. Importantly, it was able to achieve a delta-v of 4.3 km/s. That's a record.
The Future of Propulsion Technology
Are there other types of propulsion systems that could be developed to provide an efficient and economical method to power interplanetary travel?It wasn't that long ago when the prospects for nuclear rocket technology seem to be the future. Perhaps it still is.
A nuclear rocket is simply another type of reaction engine where propellant gas (stored as liquid hydrogen) is thermally heated by a nuclear reactor and expelled out the rear from the nozzle providing efficient forward thrust. Or it could be a nuclear reactor supplying the electrical energy required for an ion thrust system. Both of these systems would be effective in deeper space where electrical energy harvested from solar panels is less efficient in the dim sunlight of deep space.
In the late 60s and early 70s NASA had a program known as NERVA. That stood for Nuclear Engine for Rocket Vehicle Application. It was a demonstration of a nuclear thermal rocket engine that proved that this type of propulsive technology was efficient and practical.
NERVA designs [Fig. 12] have very favorable thrust to weight ratios. They theoretically outperform the most advanced chemical reaction rockets on the drawing boards. This design of rocket can burn for hours and is limited only by the volume of propellant on board. Potentially, it is capable of pretty dramatic delta-v and has many the advantages of both ion and chemical rockets.
Unfortunately, the NERVA program fell victim to the budget ax in the Nixon administration. There are safety and environmental concerns however when considering the launch of nuclear material into orbit. If everything goes well this technology has a lot to offer but if something goes wrong during the boost phase we could be looking at an environmental disaster. The benefits certainly have to outweigh the disadvantages when considering a NERVA type application. I think we will see it again. [Robbins 1991]

Figure 10 NERVA schematic [NASA]
Sailing
I mentioned solar sails because no review of interplanetary propulsion systems would be complete without their mention. Solar sails are a completely passive system relying on light pressure from the Sun (or from a fixed point laser) to provide thrust to carry the probe out into the solar system. But unlike a sailing ship in a fluid environment a solar sailboat is incapable of tacking or sailing into the "wind." It is an outbound system only.In 2010, a craft using solar sail propulsion was successfully launched. It was called IKAROS.
The disadvantages of solar sails are that the thrust produced is minimal and decreases by the square of the distance. The sails have to be enormous! To produce any useful thrust their areas need to be measured in square kilometers. Mission times are measured in decades not years.
One application where solar sails may be useful would be in helping to save the planet. Let's say we discovered a near earth orbiting (NEO) asteroid with the trajectory that could possibly send it on a collision course with the Earth. Given enough time, we may be able to install solar sails on the asteroid so that sunlight alone would give it that extra tiny nudge to move the asteroid into safer orbit.
Mass Drivers
The last system to be discussed in this essay may be most useful for the propulsion of larger masses such as asteroids given enough power. Let's say again we have to divert an Earth- killing asteroid or perhaps we want to put a metal-rich asteroid into a stable parking orbit so that it can be mined for its metals efficiently. If the asteroid had a high enough iron content it could be mined in useful chunks. Those chunks of iron could then be propelled into space for later collection by an electromagnetic rail gun installed on its surface. That would create a reaction force that could be used to steer the asteroid into safer or more useful orbits. The freefalling chunks could be harvested.Spacefaring
What used to be the realm of science fiction writers and then pioneering seat-of-the-pants explorers is now a robust and practical technology that will define our species in centuries to come. We are at the dawn of the first known species to become spacefaring.References:
FAA INTERPLANETARY TRAVEL 4.1.6 www.faa.gov/.../Section%20III.4.1.6%20Interplanetary%20Travel.pdfJohns Hopkins University (December 4, 2008). "Deep-Space Maneuver Positions MESSENGER for Third Mercury Encounter". PR. Retrieved 2010-04-20.
JPL. Jet Propulsion Laboratory THE BASICs OF SPACE FLIGHT http://www2.jpl.nasa.gov/basics/bsf4-1.php
McAdams, J. V.; J. L. Horsewood, C. L. Yen (August 10–12, 1998), "Discovery-class Mercury orbiter trajectory design for the 2005 launch opportunity", 1998 Astrodynamics Specialist Conference, Boston, MA: American Institute of Aeronautics and Astronautics/American Astronautical Society, pp. 109–115, AIAA-98-4283,
Minovitch, M. (1997) JPL. THE INVENTION OF GRAVITY PROPELLED INTERPLANETARY TRAVEL from http://www.gravityassist.com/IAF-4.htm
NASA/JPL Interplanetary Superhighway http://www.nasa.gov/mission_pages/genesis/media/jpl-release-071702.html
Robbins, W.H. and Finger, H.B., "An Historical Perspective of the NERVA Nuclear Rocket Engine Technology Program", NASA Contractor Report 187154/AIAA-91-3451, NASA Lewis Research Center, NASA, July 1991
Sellers, J. (2005) UNDERSTANDING SPACE 3rd Ed. ISBN 978-0-07-340775-3
Wikipedia 2011 Hohmann Transfer Orbit http://en.wikipedia.org/wiki/Hohmann_transfer_orbit
No comments:
Post a Comment